Llevo doce años impartiendo clases de matemáticas, con la fortuna de haber trabajado en casi todos los niveles; actualmente trabajo en bachillerato y educación superior, y es ahí donde nunca falta la pregunta de algún estudiante sobre la aplicación de esta ciencia en la vida real. Los alumnos son inquietos sobre los desarrollos matemáticos que involucran el uso de fórmulas y procedimientos algebraicos extensos, y esto conduce a que se pregunten cosas como: ¿Dónde aplico en mi realidad un binomio al cuadrado?, por ejemplo.
Lo importante es no dejar de hacerse preguntas.
Albert Einstein.
Aterrizar la teoría en la práctica
Es así que mi experiencia me ha llevado a reconocer que es responsabilidad de nosotros; los profesores de matemáticas, aterrizar los conocimientos matemáticos que se transmiten en un salón de clases, y si está dentro de las posibilidades, compartir ejemplos de su aplicación en el entorno real.
Como punto fundamental debemos tener en claro que las matemáticas forman parte de nuestra vida diaria, al usar los números (que son los pilares de esta ciencia formal) comenzamos a trabajar con ellas, por lo tanto, la vemos inmiscuida en prácticamente todas las actividades del ser humano, en todo lo cotidiano y de ámbito social. Por mencionar algunos ejemplos; en las cuentas que realizamos de los gastos que tenemos, nos comunicamos mediante números (son una especie de lenguaje), los encontramos afuera de los domicilios, en el transporte público, en la camiseta de nuestro jugador favorito de futbol, y no se diga el tiempo el cual es medido y cuantificado.
De la matemática debemos decir que es una herramienta imprescindible, importante, una especie de patrimonio para la humanidad, pues ha sido estructura y eje fundamental para los avances científicos y tecnológicos. Bajo esa premisa, es necesario sembrar el interés en nuestros alumnos por las matemáticas en un esfuerzo persistente que haga aterrizar la teoría en la práctica.
Según comentan, fue el mismo Gauss, uno de los matemáticos más prolíficos de la historia, quien afirmó en alguna ocasión: “Los encantos de las matemáticas, solo se le revelan a los que tienen el valor de profundizar en ella”.
También la Matemática Iraní, Maryam Mirzakhani, nos dejó una máxima como bandera: “La belleza de las matemáticas sólo se muestra a los seguidores más pacientes”.
Profesor, ¿dónde encuentro el Teorema de Pitágoras en mi casa, en el hospital o en la oficina?
Cuando los estudiantes me plantean este tipo de preguntas les respondo, primeramente, con la justificación de estudiar matemáticas. Les afirmoque son necesarias. Hacen que pensemos y reflexionemos, que mantengamos una actitud crítica de los fenómenos del entorno social y natural, al estudiarlas, nos ayudan a ‘remover el polvo’ de nuestra mente, a razonar. Son una especie de ‘gimnasia’ para el cerebro y les insisto que no solo el cuerpo requiere de ejercicio.

Luego, les invito a reflexionar sobre su entorno, que se adentren a un viaje en donde vislumbren entidades matemáticas en su realidad inmediata.
Después de la reflexión, les platico sobre la historia de los griegos; quienes fueron grandes precursores de las matemáticas, y sus aportes como el Teorema de Pitágoras pueden brindar solución a diversas problemáticas o situaciones reales.
Se dice que Pitágoras descubrió que en todo triángulo rectángulo:
“La suma de los cuadrados de los catetos (lados menores) es igual al cuadrado de la hipotenusa (lado mayor)”.

A partir de este concepto, se posibilita mostrar a los estudiantes algunos ejemplos de aplicación del Teorema de Pitágoras en la solución de problemáticas de la vida real. A continuación, menciono algunas propuestas.
Propuesta I: ¿Cuál camino es el más corto?
Supongamos que “Pedro” se encuentra en la calle y necesita llegar al punto B partiendo del punto A. Él quiere ahorrarse pasos (que se traduce en distancia y tiempo) y solo puede elegir uno de los dos caminos posibles, ¿qué le conviene más? ¿seguir la trayectoria en rojo o la de color verde?
Se puede observar como en la situación planteada aparece un triángulo rectángulo, donde el camino en color verde representa el lado mayor o hipotenusa.
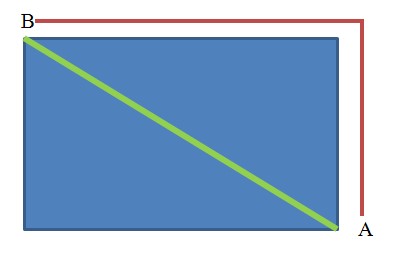
Dos posibles trayectorias forman un triángulo rectángulo.
Los alumnos, intuitivamente, deducen que la trayectoria o camino más corto es el verde, pero no es suficiente, la respuesta halla fundamento en el teorema de Pitágoras, pues al establecer la relación c2=a2+b2, los matemáticos han demostrado la desigualdad: c < (a + b), por lo tanto, a Pedro le conviene seguir la ruta verde, y así llegará más rápido a su destino.
Propuesta II: ¿Cómo asegurarnos que un muro o pared está cuadrado con el suelo?
La solución la ofrecen los matemáticos e incluso los trabajadores de la construcción. Para ello se propone: Buscar tres cuerdas cuyas medidas sean: 3, 4 y 5 unidades. Colocar las de 3 y 4 en el muro y el piso, respectivamente, si la cuerda de 5 unidades queda perfectamente sobre los extremos de las anteriores, entonces la pared está bien construida y cuadrada al piso. De lo contrario, se considera que ha quedado mal cuadrada. En la siguiente imagen se muestra una explicación mediante el teorema de Pitágoras, donde se cumple la relación: 52 = 32+42.

Cuerdas para comprobar que un muro está cuadrado con el piso.
Propuesta III: ¿Cómo calcular distancias o alturas inaccesibles?
Para calcular distancias o alturas inaccesibles es posible utilizar el teorema de Pitágoras. Por ejemplo, supongamos que queremos conocer cuánto mide un poste de alumbrado público como el que se aprecia en la imagen de abajo. Dicho poste se sujeta de un cable en forma diagonal de 5 metros de longitud y la distancia del poste a la base del cable (el cual está fijo en el piso) es de 3 metros. La solución mediante el Teorema de Pitágoras es conocer el lado vertical o cateto opuesto representado mediante la letra “a” en el esquema. Conociendo los otros dos lados [el “b” que es la distancia del poste a la base del cable (3 m) y la hipotenusa o lado “c” como la longitud del cable que sujeta al poste (5 m)], la altura del poste sería de 4 metros, como se demuestra a continuación.
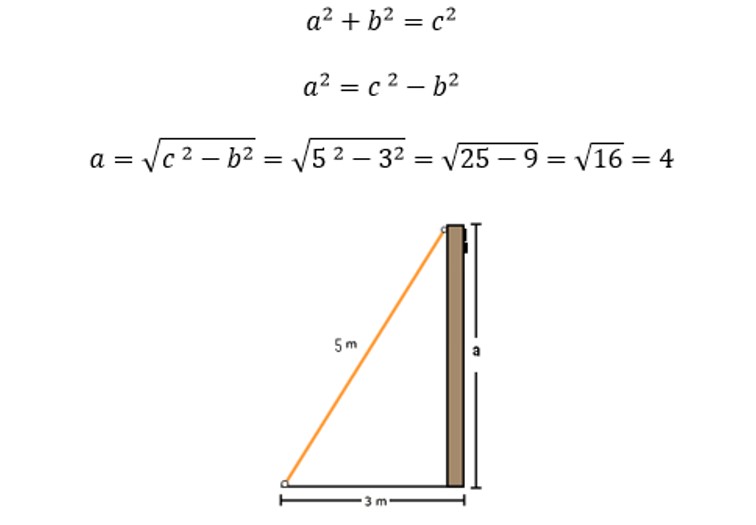
Estimación de la altura de un poste de luz.
Como vemos, el teorema de Pitágoras es, tan solo, un concepto que ofrece diversos casos de aplicación en el entorno real.
Dice Palencia, en su ensayo ‘Y Las matemáticas aplicadas ¿En que se aplican?‘, que el avance en el conocimiento matemático ha estado, generalmente, ligado a las necesidades de los diferentes aspectos de vida del hombre. En la actualidad, y hacia el futuro, las matemáticas encuentran aplicaciones cada vez en más campos.
Según Canavelli y colaboradores, en su publicación ‘Tics, Teoría de Números y Formación Docente ‘, la Matemática está en la base de los desarrollos científicos, particularmente en la Teoría de Números que fundamenta muchas de sus tecnologías en el procesamiento de la información y la comunicación.
A continuación, se mencionan algunas aplicaciones de las matemáticas en diversas disciplinas:
- Medicina. En técnicas para plasmar imágenes, por ejemplo, de lo que hoy se conoce como tomografía.
- Telecomunicaciones. Es imperante transmitir datos entre dos lugares de manera eficiente, rápida y de forma segura.
- Las computadoras y los medios de comunicación e información .Desarrollo de Internet, este vocablo ha permeado a todos los estratos socioeconómicos y a todas la edades, ha pasado de ser un vocablo que pocos entendían a un vocablo que es sinónimo de consultar, socializar, trabajar, comunicar, compartir, controlar, vender, comprar, etc.
- Física fundamental. Las matemáticas del mundo atómico y de las partículas elementales.
- Ingeniería. Procesos de la siderurgia, altos hornos. Prototipos de la industria automovilística (fluidos, aerodinámica, materiales y teoría de la fractura).
- Problemas de recursos y minería. Problemas de conservación del medio ambiente. Las ecuaciones de la extracción de petróleo, de la filtración en los suelos, de la difusión de contaminantes.
- Química. Simulación de la estructura atómica y molecular a partir de las ecuaciones fundamentales. Dinámica de reacciones. Matemáticas de la nucleación y crecimiento de cristales.
En conclusión, las matemáticas puras encuentran, cada vez más, aplicaciones en el entorno, satisfaciendo alguna necesidad o dando soluciones a los problemas. Por ello, dejo por aquí algunas reflexiones y recomendaciones:
- Aterrizar la teoría matemática es responsabilidad del docente y éste debe fomentar una cultura de la práctica; es en el teorema de Pitágoras donde podría encontrar un terreno fértil para estos fines.
- Las Matemáticas son imprescindibles en nuestro diario vivir, por lo tanto, es de suma importancia dominarlas y entenderlas; como lenguaje y herramienta nos permiten entender e interpretar los procesos y fenómenos de la vida real.
- Debemos estudiar con profundidad nuestro alrededor y apreciar más las aplicaciones de la matemática. Esta ciencia se deben de usar y desarrollar de manera continua.
- Debemos reconocer que la Matemática es la base de los desarrollos tecnológicos.
Bibliografía consultada
-Pineda, D.J. (2009). Las Matemáticas En Nuestro Mundo Cotidiano. Revista Digital Universitaria, volumen 10 Nº 1, 1-8.
-Vásquez, J.L. (2013). Las Matemáticas y Sus Aplicaciones Ayer, Hoy y Futuro. Revista Encuentros Multidisciplinarios. Universidad Autónoma de Madrid España, Nº45, 1-11.
-Palencia, V.J. (2008). Y Las matemáticas aplicadas ¿En que se aplican? [En línea], Recuperado el 1 de Noviembre de 2019 desde www.inteligencianet.com
-Canavelli, J. C., Gaitán, M.M., De Carrera, E. (2009). Tics, Teoría de Números y Formación Docente [en línea]. Argentina: Facultad Regional Paraná de la Universidad Tecnológica Nacional, Recuperado el 28 de Octubre de 2019, desde teyet-revista.info.unlp.edu.ar

Autor: José de Jesús Camacho Medina
Ingeniero en Sistemas Computacionales realizando una Maestría en Matemática Educativa con Línea de Investigación en Matemática Aplicada en la Universidad Autónoma de Zacatecas, México. Se ha desarrollado como Catedrático de diversas instituciones de nivel medio y superior, y es miembro fundador de la Sociedad Científica Fresnillense A.C. que tiene por objetivo divulgar la ciencia en el municipio de Fresnillo, Zacatecas.
Tw @pepe9mx
Cita este artículo de la siguiente forma:
